Keepig in mind the postulates of Born Theory, Born equation is derive by studying thermodynamic cycle to calculate the work
done in transferring a charged sphere from vacuum into the solvent. According to born equation the ion, represents as a charged sphere of radius R, considered to be initially place in a vacuum, and the work done Wd required to strip the ion of its charge q = Zie (discharging of ion) is determine. Then this uncharge sphere is transfer into the solvent of dielectric medium. And the work is done in transferring the ion Wtr is 0 (no work done takes place). Thus, transfer process involves no work.
Then the charge on the sphere inside the solvent is restore to its full value q = Zi e (where “e” is the magnitude of the electronic charge). And in charging the discharge sphere in solvent, work done Wc is determine. Finally, the ion is transfer from the solvent back into vacuum. The work done in this transfer process is – Δ Gs. During the whole thermodynamic cycle, the solvation energy (Esolv) is the difference in the energy of charging the sphere of radius R to charge Zi e in both vacuum and medium with a dielectric constant ε.
In the event (thermodynamic cycle) of movement of ion from vacuum to continuum dielectric solvent condensed phase, the algebraic sum of all work done is zero i.e.
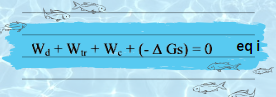
By evaluating the work done in charging an ionic sphere of radius R, from q = 0 to q = Zi e, an infinitesimal amount of charge dq is add to sphere unless the final charge level is attain.
The product of electrostatic potential 𝚿 and charge increment dq gives the work increment dw which is:
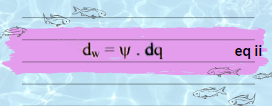
As, the total work done in charging the sphere is obtain by taking sum of all the little increments dw. Therefore, by integrating equation no. ii we get:

From fundamental electrostatics we recall from Born Theory. The electrostatic potential at a certain point in space is define as the work done to transport a unit positive charge from infinity to that specific point. Now the electrostatic potential at a point located at distance r from charged sphere 𝚿 (r) is given by the product of the electric field strength E(r). Electric field strength defines the electric force per unit charge acting on the moving test charge and the distance r through which the charge is carried.
So, the equation become as:

Since the electric field E, at a distance r from an ion of charge q= Zi e (and radius R) has magnitude Zi e/ 4𝝿𝝴o and dr =2R. Therefore, by putting the value of equation iv in equation iii, we get:

By solving integration:

Whereas, Zi = charge on an ion.
e = magnitude of the electronic charge.
𝝴o = permittivity of vacuum.
R = radius of ionic sphere
It is well-know that work done in discharging of ionic sphere is negative of work done in charging a sphere. Therefore, the equation of discharging of sphere is:
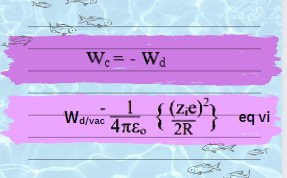
Contrary, the work done on the recharging of ionic sphere when it enters into dielectric solvent is given as:

simplifying the above equation by taking only the relative permittivity of dielectric continuum:

Solvation energy is usually express as the difference in work which results from ion charging in both vacuum and liquid phase. Therefore, born ascribes the change in energy and give expression for Gibbs free energy of solvation as:

So, by putting the value of Wd and Wc from equation number vi and vii, we get the final born equation as:
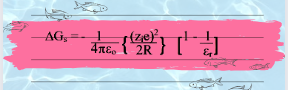
Further simplification gives equation:
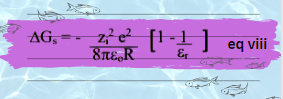
Equation viii is the final Born equation for free energy of solvation. It is also express in molar Gibb’s free energy, because above equation depicts charging of only one particle. Whereas, in the molar gibs free energy, above equation obtained is multiply by the Avogadro number to calculate the charging energy per one mole.

Whereas, εr = relative permittivity or dielectric constant, the factor by which electrostatic potential energy of interaction between the charges is decrease in continuum dielectric medium.
Now since the dielectric constant is εr > 1 always and so 1/εr < 1 then Δ Gs will always be negative.
Born Equation & Enthalpy and Entropy of ion solvation.
Although Born equation for free energy of solvation (i.e. above equation number viii) is the work obtain by transferring a charged sphere from vacuum to condensed medium. The work displays itself in solvation heat. Since the system temperature T is constant, the heat emitted passes to a thermostat. It is assume then that Born has taken solvation energy as the change in either internal energy or enthalpy upon solvation. However, the Gibbs free energy calculated by Born is the maximum work perform by electric forces durring ion dissolving. Therefore, equation viii is equate with the change in the Gibbs energy which further allowed to calculate solvation enthalpy as well as entropy. In accord with the Born equation, ΔH and ΔS is obtain from a relation:

Born equation deals with the change in thermodynamic parameters (i.e. Gibb`s free energy, enthalpy, entropy) of ion when it enters from vacuum into continuum dielectric medium, so by rearranging above equation we get:
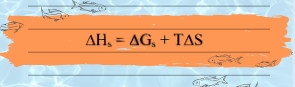
The Entropy of solvation needs to be calculate first in order to calculate the enthalpy so:
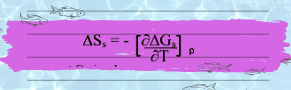
By putting value of ΔGs in above eq we get.

To calculate Born enthalpy of solvation, we put the value of eq ix in above equation of Δ Hs.

Here, eq. x is the born calculation of enthalpy of ion solvation from vacuum to continuum
dielectric medium.
