Born Model Of Ion-Solvent Interaction. The Theory Of Solvation

 A Born model explains classical electrostatic ion-solvent interaction

Introduction to Born Model of Ion-Solvent Interaction.

Before discussing Born model of Ion solvent interaction lets chech who is Max Born. Max Born (1882-1970) was one of the founding fathers of modern quantum mechanics, having proposed the probability interpretation of the wave function, for which he ultimately obtained a Nobel prize. One of his pioneer works became the starting point for most discussions of the thermodynamics of ion solvation in 1920; he developed a model in which he gives detailed studies of physical electrochemistry while considering the solvation of ions in electrolytic solution with a significant focus on ion-solvent interactions.

The Birth of Born Theory of Ion Model.

To recognize the quantitative behavior of electrically charged moiety in condensed phases has taken a central place in physical chemistry for over a century. Aside from modern statistical mechanical theories of electrolyte solutions use recently to give a detail picture of the molecular structure of solute and solvent molecules and potentials, which describe the interactions between these species and emphasize detail atomic models. Still continuum electrostatic theories are widely employ to interpret experiments; with respect to the biophysical chemistry of macromolecular solutions, and discuss the progress that has been made in the understanding of nature and structure of solvated ions. 

The strength of continuum models lies in the relative ease with which formulas may be derived and applied. However, in this regard, the born equation derive by born theory, also known as structureless continuum dielectric theory, plays a vital role in determining simpler phenomenological equations that are useful to interpret the results for complex systems by considering different thermodynamic functions, such as the free energy of solvation, enthalpy, and entropy that has been applied to many problems in solution chemistry and biophysics.

Born Theory Definition.

 “Based on an electrostatic model that treats the solvent as a continuous dielectric medium, the Born theory estimates the electrostatic component of Gibbs free energy of solvation of an ion along with the enthalpy and entropy of solvation system.”

 OR

“A blend of classical electrostatic and thermodynamic cycles that tend to take place when an ion from a vacuum enters into a condensed dielectric polar medium/solvent i.e. water is what known as Born theory.”

Such interaction may also occur with organic solvents like (alcoho, phenol etc.).

Born Equation.

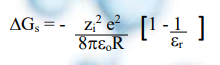
Born Model of Ion-Solvent Interaction.

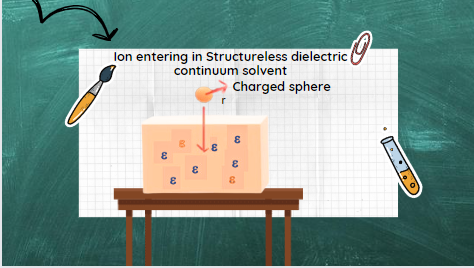
The Born model, proposed in 1920, represents the most straightforward continuum theory of ionic solvation. It is an approach develop by Born that can be use to model the energetics of ion-solvent interactions conveniently. The born model is basically a continuum approach representing simple, interpretable, and computationally inexpensive physical calculations. Such calculations do not involve many adjustable parameters. Such a model is use to calculate the excess free energy of solvation of spherical ions. It is based on classical electrostatics and represents the solvent as a structureless dielectric continuum. Through this model, born assigns the change in energy (i.e., free energy -ΔG) by the modification of the energy content of the surrounding medium, which is a vacuum initially and a continuous dielectric of permittivity (ε) finally.

Explaining Born Model.

The Born model is a simple approach for quantifying a series of events that occurs when an ion enters from a gas phase into a polar solvent (such as water). Hence it is solvated. Born used classical electrostatics to evaluate the free energy change upon the transfer of ions from the vacuum to the solution.

In this straightforward model, the ions are represent as charged hard spheres. Whereas, the solvent is consider as a structureless fluid with uniform/continuum macroscopic dielectric. This is unperturbed even in the presence of ionic fields.

Solvent (Water) as a Structureless Fluid.

In his model, Born adopts a very simple first-order approach and assumes that the solvent medium does not have a molecular structure. Instead it can be regard as a structureless dielectric continuum into which ion is embed as a charged sphere. The reason why the Born model uses a structureless solvent is that water molecules act as a dipole. When an ion enters into this solvent, it will interrupt its dipolar host (i.e., solvent/water). This interaction is not simple and causes a significant change in the structure of water. The spherically symmetric electric field of the ion can tear water dipoles out of the water lattice and make them point or orient with the appropriate charged end towards the central ion. Because of the operation of these ion/dipole forces, three types of ion-solvent interactions take place.

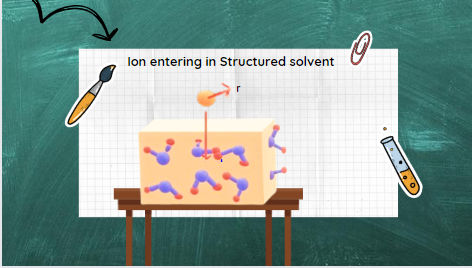
Types of Ion-Solvent Interactions.

1. A certain number of water molecules in the immediate vicinity of the ion may be trap and orient in the ionic field. A solvent sheath of orientated, immobilized water molecules envelops ions. These immobilized water molecules move with the ion as it moves through the solvent medium. The fate of these immobilize solvent molecules is tie up with that of their partner ion.
2. The secondary or structure broken region (a bit away from ion) where the bulk structure of water breaks down to various degrees. Hence, this distorted structure can not participate in ion-solvent interaction as expected.
3. At a considerable enough distance from the ion, the electric field is negligible. Thus, the solvent structure will not be affect by the ionic field. Here, the bulk water structure will pertain. The solvent molecules will not realize that the ion is there at all. Therefore, it can not take part in ion-solvent interactions.

Concluding the matter.

On the basis of these observations, Born concludes that in the region between the solvation sheath (where the electric field of the ion determines the water orientation) and the bulk water (where the orientation of the water molecules is unaffect by the electric field of the ion), the orientating influences of the ion and the water network operate in a microscopic pull of war. The former tries to align the water dipoles parallel to the spherically symmetric electric field of the ion. In contrast, the water network tries to make the water molecules continue adopting the tetrahedral bonding arrangement. This is necessary for membership in the network structure.

Hence, caught between the two types of influences, the water in this “in-between” region seeks to adopt a compromise structure. Hence the structure is neither completely orient nor disorient. Therefore, the Born model of ion-solven interaction approaches structureless dielectric continuum solvent in which the spherical charge ion is enter. Aside from using a structureless dielectric continuum solvent, when compared with experimental data, the Born model yields accurate results if a proper radius for the ion is choosen. That is, the effective Born radius, R_eff, is a choise.

Statement of Born Theory.

 A born theory is a blend of classical electrostatics and thermodynamic cycles. It gives an equation that evaluates the Gibbs energy change ΔGs associated with the process of ions. Here the transfer of an ion from a gaseous vapor at low partial pressure to the desired solvent (e.g., water) takes place in the absence of any ion/ion interactions. Born theory successfully quantified the energetics of ion solvation. This is done by describing the work done in transferring a charged sphere from a vacuum into a dielectric continuum. 

Assumptions/Postulates of Born Model.

✓ The solvation proceeds spontaneously, i.e., ions prefer to be solvated than to be in a vacuum. Hence, solvation is thermodynamically favorable.

✓ In the beginning of ion-solvation, no ion-solvent interactions are present, which corresponds to the ions in a vacuum. 

✓ At the end of the ion-solvation, ion/solvent interactions were operative, which corresponded to the ion in the solution. 

✓ The ion also has structure. The born model represents the ion as a charged sphere of net charge q_i = z_ie and radius R_i. 

✓ Only charge on an ion is responsible for ion/solvent interaction. Hence, ion/solvent interactions are solely electrostatic. 

✓ the more negligible the ion (smaller R) and the larger the dielectric constant, the greater the solvation-free energy (ΔGs). 

✓ Solvent molecular effects become particularly important when estimating free energies of transfer of ions from one solvent to another. That is from vacuum to dielectric continuum. 

✓ A fundamental assumption is that the response of the solvent molecules to the charge distribution of the solute (ion) is linear. This gives rise to the quadratic dependence of the Born free energy on the solute charge. 

✓ For a spherical ion, the Born excess free energy of solvation has a direct dependence on the ionic charge q, the radius R, and the solvent dielectric constant ε.  

Drawbacks of Born Model of Ion-Solvent Interaction.

✓ The Born equation fails to describe ion solvation quantitatively in numerical form. It can be use to estimate qualitatively how solvation energy depends on the ionic size, the medium’s dielectric constant, and temperature. 

✓ One should accurately determine the initial and final states of the system in order to calculate the change in the Gibbs function. In the born equation, the charging of only one particle is discussed. The obtained results are multiplied by the Avogadro number to measure the charging energy per one mole. When compared with enthalpy, the Gibbs function is pressure-dependent in the initial state. While it depends on ion concentration in the final state. Thus, it is not possible to explain the change in the Gibbs function by the Born equation. We have generalized the Born equation for that purpose.

✓ No experimental proceedings were done to develop a microscopic interpretation of the parameters contained in this macroscopic theory.